smoothing by moving average
3. 移動平均による平滑化
単に7日周期の波を取り除くのならわざわざフーリエ変換なんかしなくてもいい方法がありそうです。ここでは7日ごとに平均をとる方法を試してみます。というか、ホントは最初に思いついたのはこちらです。んで後から「つーかそれって株価で言う移動平均と同じ操作だよな」と思い、さらに「てゆーか移動平均って要するにフィルタリングじゃん」と思ったというのが実状です。どーでもいいですね。とにかく7日単位で変動するんなら7日間の平均をとっちゃえばそんな変動はならされて消えるだろう、という目論見です。具体的には、ある日の過去3日間・その日・先3日間の合計7日間の1日あたりアクセス数の平均値をその日の値とします。計算としてはごく単純な操作ですな。平均をとる期間(ここでは7日間)が1日ずつ移動していくので移動平均と呼ばれます。
ただ、ほんとは株の世界で言う移動平均はこれと少し違い、期間が7日であるならば当日を含めた過去7日間の平均をとってその日の移動平均値とします。これはあくまでも「過去の傾向から未来の変化を予測する(そして儲ける)」という目的意識からそうしているのでしょうが、個人的にはちょっと疑問です。詳述は避けますが、そういう株価チャート式の移動平均だと結果として得られる曲線は元データと位相がずれてしまうからです。波形分析という観点から言えばこれは好ましくありませんし、実際にここでは日付との対応をとって変動の意味を推測するという目的があるので位相ズレは困ります。というか、そもそも株価チャート式移動平均でもここでやっている方法の移動平均でも結果として出てくる波形は全く同じですから、位相ズレがない分だけこちらのやり方の方がいいと思うのですが。まぁいいや。株の世界の習慣というか伝統というか、そういうものなのでしょう。
とにかく、ここでは3日前〜3日後までの平均を7日移動平均と呼んでますが、それは株価チャート式の移動平均とはちょっと違いますので誤解なきよう。以後も株価チャート式の移動平均は使いません。ってなわけで前説が長くなりましたが、まずは早速その7日移動平均の結果を見てみましょーか。
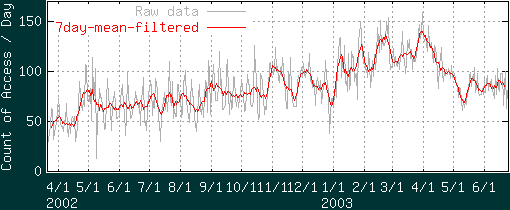
確かに週単位での乱高下はなくなっているようですけど、まだ細かいギザギザが残ってます(この大きさの画像だとわかりにくいかも知れませんが)。もっと高い周波数の成分が除去しきれてないんでしょうな(cf. 図4 )。しかーし私はあきらめません(何故かこだわる)。このページの冒頭でも書きましたが、移動平均ってのは要するに平均値フィルタリングと同じなわけです。実際、デジタル画像処理関係の本なんか見てみると平滑化フィルタとしてmeanフィルタという名前で紹介されてたりします。ここではつまり幅7日の単独矩形パルス波で元波形をフィルタリングしてるってことです。だったらそのフィルタ特性を見てやれば移動平均で何が起こってるんかわかるんじゃなかろーか、という訳で、7日移動平均フィルタ(横幅7、高さ1/7の単独矩形パルス)をフーリエ解析してみます。
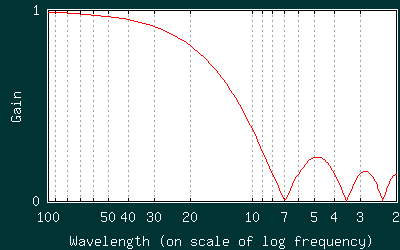
低周波数側ではなだらかなローパスフィルタとなってます。7日周期の波は完全にカットしていることもわかります。が、それより短い波長の成分をけっこう残してしまっているのもわかりますな(グラフ右方の小山)。ここがいけないわけです。どうにかしてこの小山をつぶしてやれないだろうか、と考えます。ちょうど波長5日のあたりが山になっています…ということは、5日移動平均をさらにかけてやればこの山がうまくつぶれるのではなかろうか? つまり7日移動平均をかけた結果にさらに5日移動平均をかけてやったらいいのでは? と思ったわけです。
ほな早速やってみましょ、という前に、まずはそうしたときのフィルタリングの特性を見てみます。フィルタリングというのは要するにたたみ込み積分のことなわけですが、たたみ込み積分についてはふつうのかけ算と同じように分配法則とか交換法則とか成立します。ので、 生データ*7日移動平均フィルタ*5日移動平均フィルタ という操作は、 生データ*(7日移動平均フィルタ*5日移動平均フィルタ) と同じことです(*はたたみ込みの記号)。後者のカッコの中をひとつのフィルタと見て(仮に5*7日移動平均フィルタとでも呼んどく)このフィルタ特性を考えりゃいいわけです。というわけで、その5*7日移動平均フィルタをフーリエ変換してフィルタ特性を見てみるとこんなカンジです。
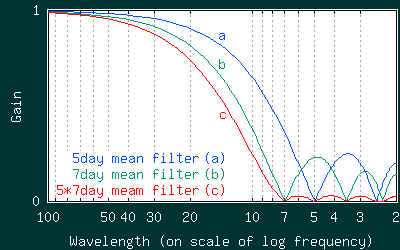
うまいこと小山がつぶれて高周波数成分がほとんどなくなっていることがわかります。信号空間でのたたみ込みは周波数空間でのかけ算に相当するので、5*7移動平均フィルタの特性(赤い線:c)は、5日移動平均フィルタの特性(青い線:a)と7日移動平均フィルタの特性(緑の線:b)の積になってます。それでうまく小山がつぶれているわけですね。かわりにローパス側の立ち上がりが若干鈍くなってますがまぁ仕方ない範囲でしょう。結果として、7日周期の波は完全に通さず、かつそれ以上の長波長(低周波数)成分は通過させるなだらかなローパスフィルタとなってます。わーい万々歳、というわけです。んじゃ早速これを使ってみましょー。生データの7日移動平均からさらに5日移動平均をとりました。結果は下の如し。
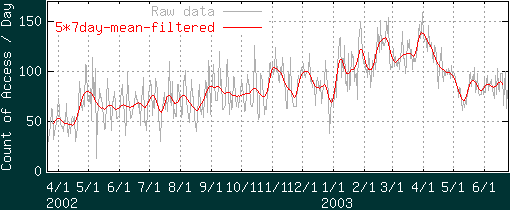
ギザギザが消えてきれいに平滑化されました。これなら大きな変化をなんとなく見てとれそーです。高周波数成分をすぱっと切ってフーリエ逆変換した結果( 図4 )と見比べても似たようなもんですな。ちなみに移動平均以外のローパスフィルタも試してはみたのですが(ガウシアンとかsincとか)、それと比べて5*7移動平均をとる方法はフィルタ特性も遜色ない(ここでの目的にかなう範囲で)ですし、そもそも計算がひじょーにラクちんなのがイイです。
とまぁそんなこんなで高周波数成分のノイズ(とくに7日周期の波)を除去することに成功いたしやした。次はグラフを眺めてあれやこれやと考えてみまっす。